So I know, it’s been a minute since I last posted. I was travelling the world and shit; I ain’t got time to be teaching when I’m kicking back cheese, chocolate, and beer all day long. Back to business.
Quadratic Formula
I don’t know how so many people memorize this goddamn monstrosity, but they do, and they likely don’t know where the fuck it came from. Fuck that. I’m going to show y’all where it comes from, building on my last post about completing the square. You should be excited about this.
The quadratic formula is used to find the solutions to quadratic equations. No shit, right? It looks like this, and I hate it:
$$x=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}$$
Alright so what is a quadratic equation? Anything that looks like this:
$$ax^2+bx+c=0$$
Graphically, that $ax^2+bx+c$ takes on a parabolic shape, like so:

Alright so what does it mean to find solutions for quadratic equations? A solution is any value for x (or whatever fucking letter/s you are using) that makes the equation true. So if we use the expression we graphed above, our quadratic equation would be:
$$2x^2-3x+1=0$$
So then, a solution to this equation would be any value for x that would make the left side of the equation equal to zero. Another way to think about a solution is any point where the graph of the equation crosses the x-axis, since those are the places where the function is equal to zero. This is also called finding zeroes, or roots, since throwing in fucking ambiguous language always helps.
So we know that the quadratic formula gives us the solutions to quadratic equations, but how the hell does it do that? Because, you eager motherfucker, all the quadratic formula is is a factored version of the same damn equation. All it is is a nasty-ass shortcut. Watch me factor this shit. I complete the square to do this, so if you ain’t up to speed on that, go learn something here.
$$ax^2+bx+c=0$$
$$x^2+\dfrac{b}{a}x+\dfrac{c}{a}=0$$
$$[x^2+\dfrac{b}{a}x+(\dfrac{b}{2a})^2]+\dfrac{c}{a}=(\dfrac{b}{2a})^2$$
$$(x+\dfrac{b}{2a})^2=\dfrac{b^2}{4a^2}-\dfrac{c}{a}$$
$$(x+\dfrac{b}{2a})=\pm\sqrt{\dfrac{b^2}{4a^2}-\dfrac{c}{a}}$$
$$x=-\dfrac{b}{2a}\pm\sqrt{\dfrac{b^2}{4a^2}-\dfrac{c}{a}}$$
$$x=-\dfrac{b}{2a}\pm\sqrt{\dfrac{b^2}{4a^2}-\dfrac{4ac}{4a^2}}$$
For fuck’s sake! I’d like to take this moment to say that deriving this shit is ugly as hell (uglier than I remembered it being) and I am going to try my damnest not to have to type anything like this clusterfuck out ever again. Anyway…
$$x=-\dfrac{b}{2a}\pm\sqrt{\dfrac{b^2-4ac}{4a^2}}$$
$$x=-\dfrac{b}{2a}\pm\dfrac{\sqrt{b^2-4ac}}{2a}$$
$$x=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}$$
Fucking done. So you can see that the quadratic formula is just a mangled-beyond-belief version of the original equation. So that means whatever we find for x using this formula is automatically a solution for the equation. You’ll notice that there’s a $\pm$ in there, which is a result of taking the square root during the derivation of the formula. This means that we may get two solutions – one using the “plus” of the $\pm\,$, and one using the “minus.” This isn’t a problem, though, because the graph above shows that the graph crosses the x-axis twice – therefore there are two solutions.
So let’s find the solutions for the original equation and be done. From before:
$$a=2,\,b=-3,\,c=1$$
So now plug them shits in and see what we get.
$$x=\dfrac{3\pm\sqrt{-3^2-4\times2\times1}}{2\times2}$$
$$x=\dfrac{3\pm\sqrt{9-8}}{4}$$
$$x=\dfrac{3\pm\sqrt{1}}{4}$$
$$x=\dfrac{3+\sqrt{1}}{4},\,x=\dfrac{3-\sqrt{1}}{4}$$
$$x=\dfrac{4}{4},\,x=\dfrac{2}{4}$$
$$x=1,\,x=0.5$$
I’ll be damned, that worked out nicely. Compare those answers with our graph, and they seem to check out, so I say we’re done with this shit.
The Quadratic Formula. A necessary evil.

This site is very informative and I felt a great relief while learning it, due to the expletive manner it was worded. Thank you for the grueling math process mixed with comedic alleviation.
I have this really wierd worksheet that I don’t understand! Using h=-16t^2+s im so confused.
This taught me more than my algebra teacher did in half a year
I still don’t get it.
He used the original equation and complete the square with it, before making x the subject
There’s some shit i don’t get. My stupid-ass teacher gave us problems in the form of
a(x)+b(x)+c and wants the answer in the form of (x +/- something)(x +/- something)
HOW THE FUCK DOES THIS WORK?!?!?!?!?
All you need to know is what a, b, and c are my mans. Once you know that just plug it in to the quadratic formula and work it out. The +/- shit comes from the equation where it says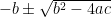 . All that means is you get 2 different answers. One from when you use + and one when you use -.
. All that means is you get 2 different answers. One from when you use + and one when you use -.
You’re a goddamned saint. I was so sick of looking at the textbook at whatever next step in solving an equation, where there was just something left out that was assumed we knew already, thinking “now how did they get THAT? Drawing a pentagram around a burning pile of math books and selling their soul to satan for the power to rub my ignorance in my face?” Anyway. I think your explanations are very helpful and because of the way in which they’re presented I think they will be much easier to recall when I need them. Also, thank you for fucking explaining the “complete the square” idea. There was an explanation in the textbook involving the square ( it was a historical example involving the creation of a box made of a square sheet of tin with smaller squares that had been cut from the corners etc) and it helped me visualize the idea sort of, but the equations that went with it were hard for me to connect to the modern version. I just kept staring at it and re-reading and still not quite grasping the implications and the fact that it lead into the quadratic formula. That period of frustration culminated in my asking google for help and ending up here. Please keep it up, it looks like I’m not the only one getting some much needed alternative insight into these things. Seriously. Thank you.
You taught me this in 5 minutes, my Algebra teacher couldn’t do it in 45 minutes. Thank you so much
that’s the answer i was looking for:
a recumbobbulated version of the original problem to find ‘x’.
that it’s not something new but an already processed version of something we do with every other math problem to find for ‘x’, then gave it a special name much like we did with pi; pi being just another ratio.
i really appreciate this
HOW THE FUCK DO I FIND A IN ONE OF THESE BITCHES